Convolution Neural Networks (CNNs) have been successful in solving common problems related to computer vision tasks, resulting in remarkably low test errors for tasks like image classification and object detection. Despite the success of CNNs, they have several drawbacks and limitations. Capsule Networks address these limitations.
CNNs extract features of an image in steps. Layers near the start detect simple features like edges and shapes, and deeper layers detect high-level features like eyes, noses, or an entire face. And finally, the network predicts the object.
The Max Pooling operation in CNNs causes the loss of most information about spatial relationships (like size and orientation) between the layers. The loss of information about orientation makes the model susceptible to getting confused.
Capsule Networks tries to solve the limitations of CNNs by preserving information and, as a result, has achieved an accuracy score of 99.87% on the MNIST dataset.
This blog will explain the workings of Capsule Network, created by Geoffrey Hinton and his machine learning team.
Limitations of CNNs
- Loss of spatial information: CNNs use pooling operations like max-pooling to reduce image size and create ian mage representation. This helps the model to achieve translational invariance (recognizing objects regardless of position). However, this discards valuable information about an object’s parts and their arrangement.
- Viewpoint variance: CNNs struggle with recognizing objects from different viewpoints (rotations, translations, and slight deformations). To address this issue, the model is trained on a huge amount of augmented data (original data edited, rotated, stretched, etc), forcing the model to learn the variation of an image, moreover, this is a brute-force approach.
- Part-Whole Problem: The artificial neuron network (ANN) excels at recognizing patterns within images. However, they struggle to represent relationships between different parts of an object (how different features combine to form an object). Pooling operations discard spatial information, making it difficult for CNNs to understand how, for example, a leg connects to a torso in an image of a dog.
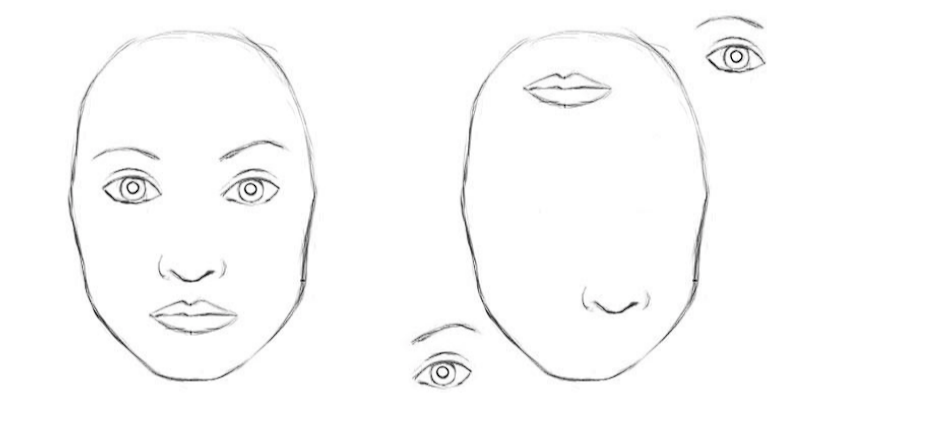
Examples Where CNNs Struggle
CNNs miss the bigger picture when parts are hidden, twisted, or viewed from unexpected angles. Here are a few examples that would likely cause CNNs to struggle.
- Hidden Parts: A fence hiding a dog’s body confuses CNNs.
- New Viewpoints: A CNN trained on upright cats might miss a lying-down cat because it can’t handle the new pose.
- Deformations: If trainers train a CNN on faces with neutral expressions, it will struggle with faces showing strong expressions (wide smiles, furrowed brows) because the CNN lacks understanding of the spatial relation between facial features when altered.
What are Capsule Networks?
A Capsule Network is just a Neural Network that improves the design of CNNs by the following key changes:
- Capsules
- Dynamic Routing, routing by agreement, and Coupling Coefficients
- Squashing Function
- Margin Loss Function
While CNNs achieve translational invariance (recognizing an object regardless of position), Capsule Networks aim for equivariance. Equivariance considers the spatial relationship of features within an object, like the position of an eye on a face.
What is a Capsule?
At the core of Capsule Networks is the concept of a capsule, which is simply a collection of neurons. This set of neurons, called a capsule, outputs a vector.
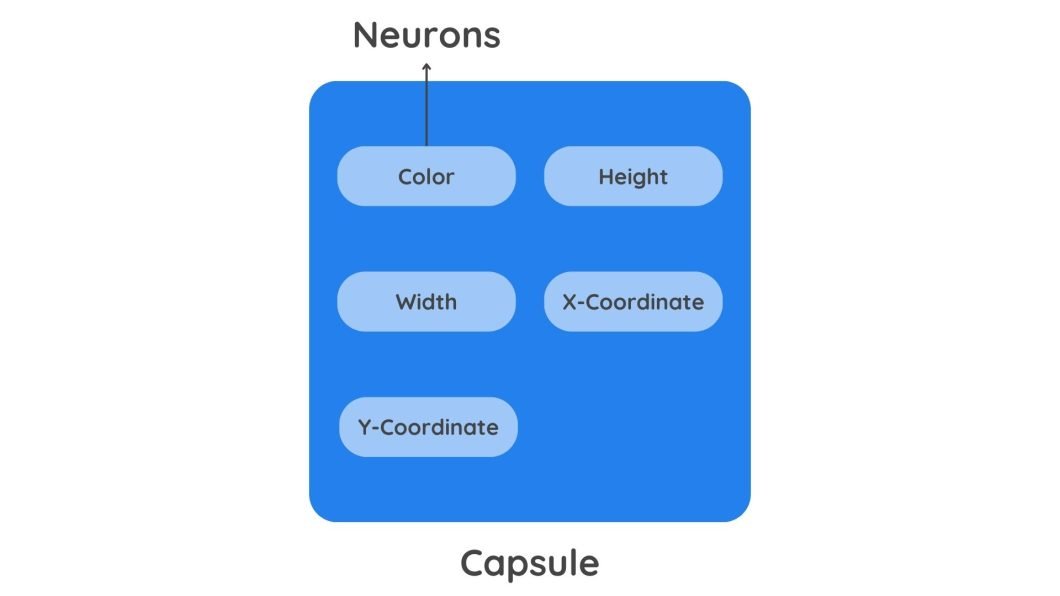
In traditional neural networks like CNNs, neurons are scalar output units (weighted sum) that represent the presence of a feature through their activation values. However, a capsule outputs a vector with detailed information. This extra information helps Capsule Network understand the pose (position and orientation) of an object’s parts, along with their presence.
Here is the additional information the output vector of the capsule holds:
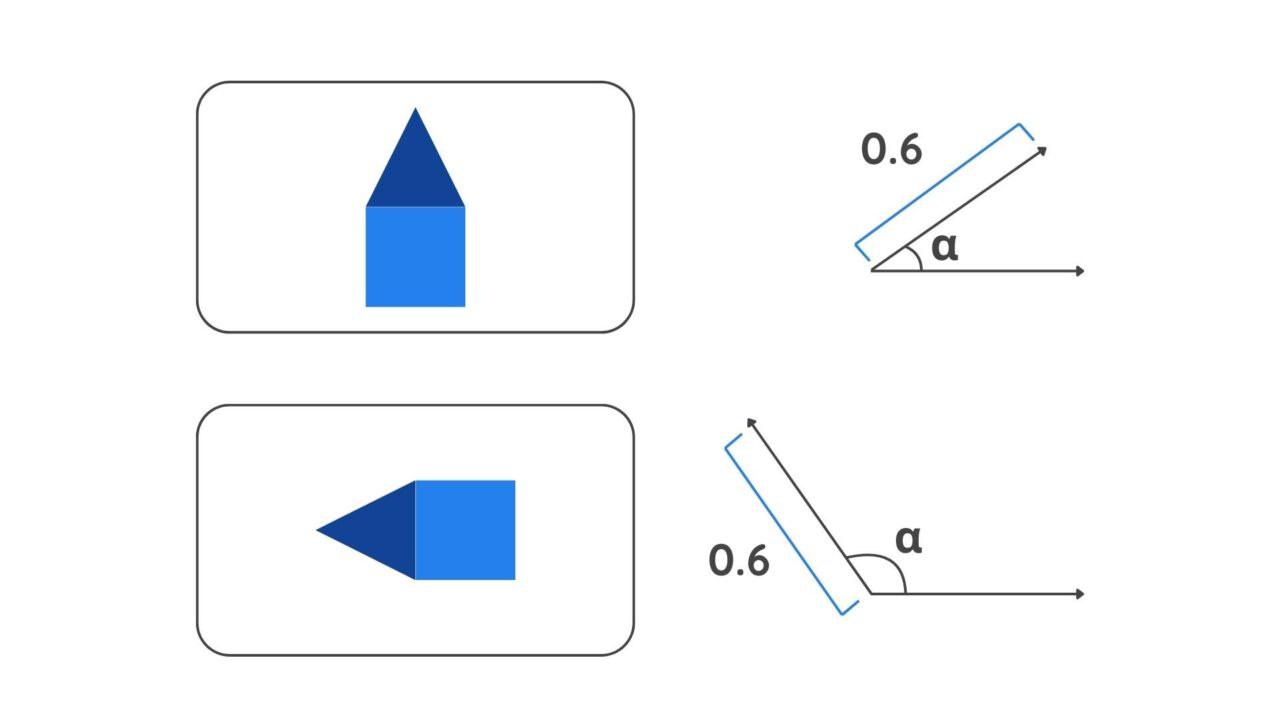
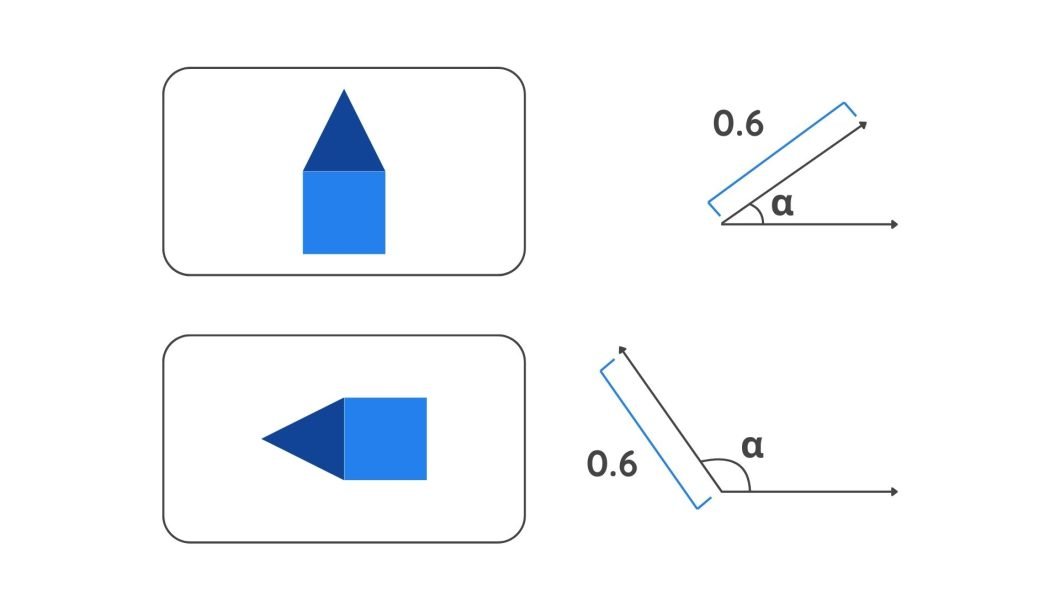
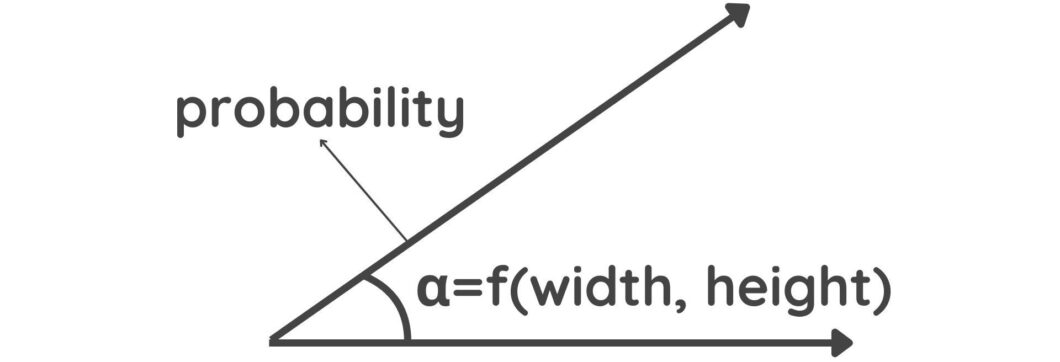
- Pose Information: A capsule outputs a vector that contains additional information such as position and orientation. This information is coded in the angle of the vector. A slight change in the object’s features will result in a different angle value.

A diagram depicting vectors - Strength: The probability of a feature’s presence is indicated by the length of the Vector. A longer vector length means a higher probability.

Capsule output vectors
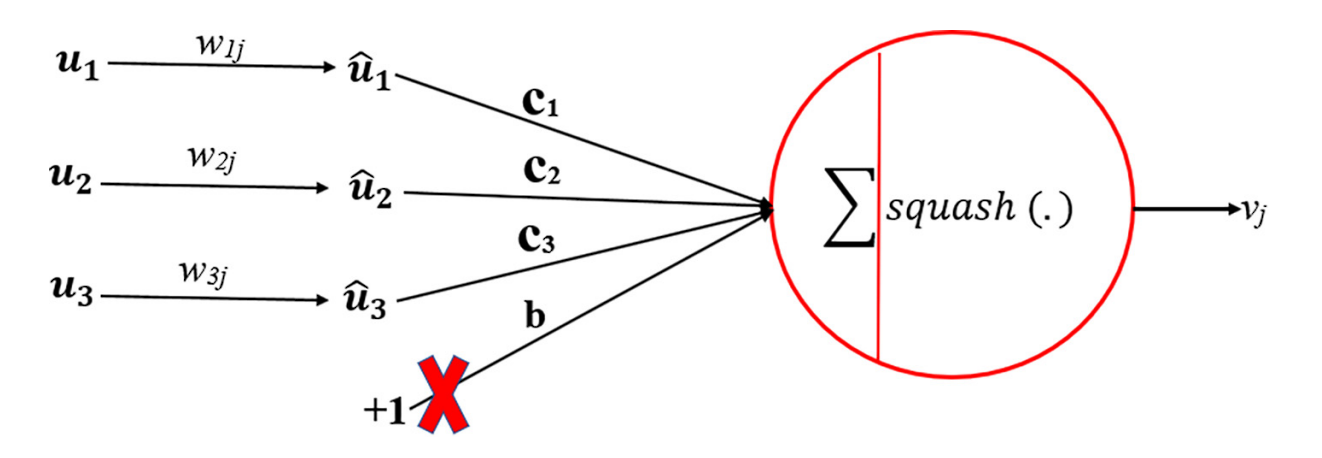
What is Dynamic Routing?
Convolutional Neural Networks (CNNs) primarily focus on just the individual features within an image. In contrast, Capsule Networks understand the relationship between individual parts of an object and the entire object. It knows how parts of an object combine to form the actual object, also called the part-whole relationship. This is possible due to the dynamic routing process.
The dynamic routing process ensures that lower-level capsules (representing parts of objects) send their output vectors to the most appropriate higher-level capsule (representing the whole object). This allows the network to learn spatial hierarchies in turn.
| Routing Algorithm | |
|---|---|
| 1: | procedure ROUTING(u^j|i, r, l) |
| 2: | for all capsule i in layer l and capsule j in layer (l + 1): bij ← 0. |
| 3: | for r iterations do |
| 4: | for all capsules i in layer l: ci ← softmax(bi) |
| 5: | for all capsule j in layer (l + 1): sj ← Σiciju^j|i |
| 6: | for all capsule j in layer (l + 1): vj ← squash(sj) |
| 7: | for all capsule i in layer l and capsule j in layer (l + 1): bij ← bij +u^j|i •vj |
| return vj | |
Routing Algorithm – source
What is a Coupling Coefficient
Coupling coefficients (cij) are scalar values that determine the strength of the connection between a lower-level capsule and a higher-level capsule.
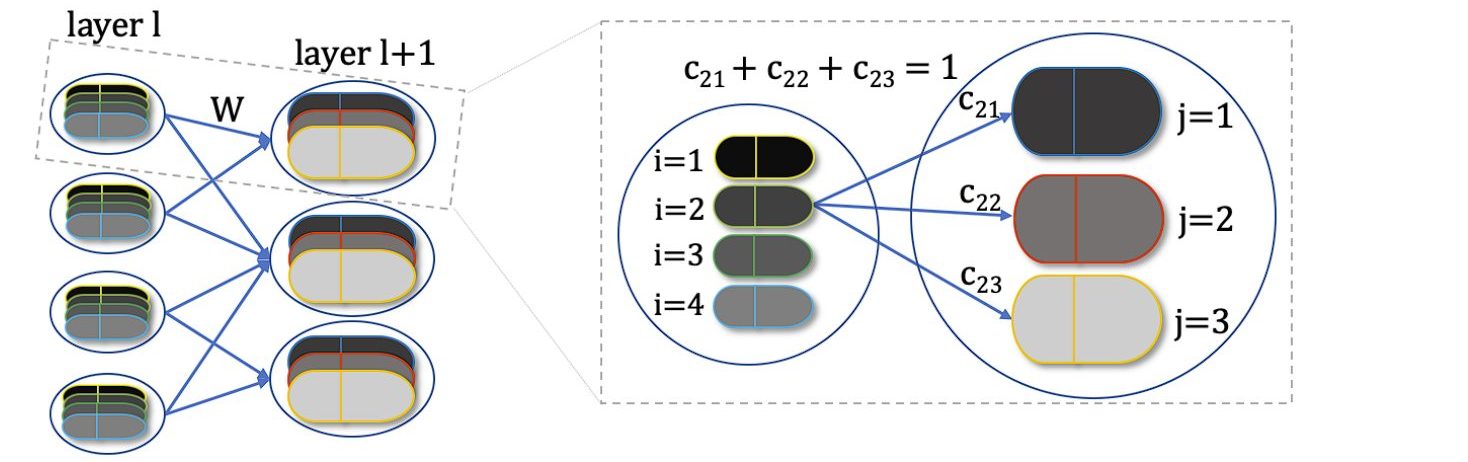
They play a crucial role in the dynamic routing process by guiding the amount of output from the lower-level capsules sent to each higher-level capsule. The dynamic routing algorithm updates cij indirectly by the scalar product of votes and outputs of possible parents.
What is the Squashing Function?
The squashing function is a nonlinear function that squashes a vector between 0 and 1. Short vectors get shrunk to almost zero length, and long vectors get shrunk to a length slightly below 1. This allows the length of the vector to act as a probability or confidence measure of the feature’s presence, without losing the vector’s direction.

What is the Margin Loss Function?
In Capsule Network, to accommodate vector outputs, a new loss function is introduced: the margin loss function.
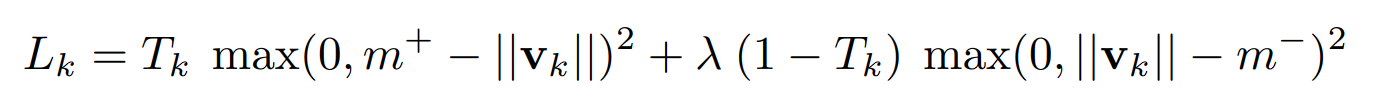
- Lk: The loss for capsule k, which corresponds to a specific digit class (e.g., the digit “2”).
- Tk: A binary indicator that is 1 if the digit class k is present in the image, and 0 if it is not. This allows the network to distinguish between digits that are present and those that are not.
- ∣∣vk∣∣: The magnitude (or length) of the output vector of capsule k. This length represents the network’s confidence that the digit class k is present in the input.
- λ: A weighting factor (set to 0.5) is used to down-weight the loss for digit classes that are not present. This prevents the network from focusing too much on minimizing the presence of absent digit classes, especially early in training.
The total loss for an input is the sum of the Marginal Losses (Lk) across all digit capsules. This approach allows the network to learn to correctly adjust the lengths of the instantiation vectors for each capsule, corresponding to each possible digit class.
Training A Capsule Network
Forward Pass
- Preprocessing and Initial Feature Extraction: The first layer of the Capsule Network is a convolution layer that extracts features like edges and texture and passes them forward to the capsule layer.
- Primary Capsule Layer: This is the first capsule layer. Here, local features detected by the convolutional layers are transformed into vectors by the capsules. Each capsule in this layer aims to capture specific features or parts of an object, with the vector’s direction representing the pose or orientation and the length of the vector indicating the probability of the feature’s presence.
- Squashing Function: The squashing function preserves the direction of the vector, but shrinks the vector between 1 and 0, indicating the probability of a feature’s presence.
- Dynamic Routing: The dynamic routing algorithm decides which higher-level capsule receives outputs from the initial capsules.
- Digit Capsules: The capsule network’s final layer, known as the digit capsule, uses the output vector’s length to indicate the digit present in the image.
Backpropagation
- Margin-based Loss Functions: This function penalizes the network when the agreement between a capsule and its most likely parent (based on pose) is not significantly higher than the agreement with other potential parents. This indirectly encourages the routing process to favor capsules with stronger pose agreement.
- Weight Updates: Using the calculated loss and gradients, the weights of the neurons in the capsules are updated.
For multiple epochs over the training dataset, the process repeats the forward pass and backpropagation steps, refining the network’s parameters each time to minimize the loss.
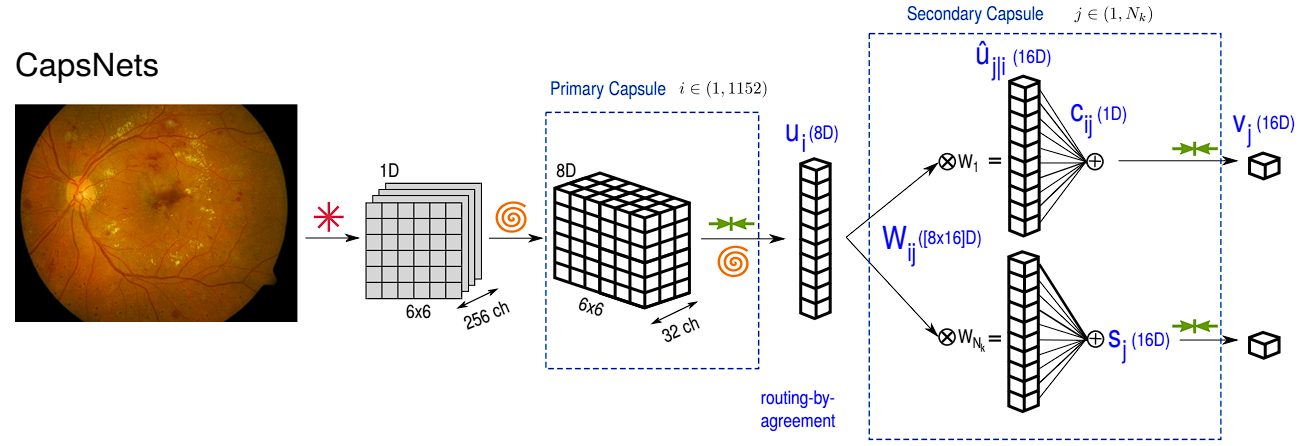
Capsule Network Architecture
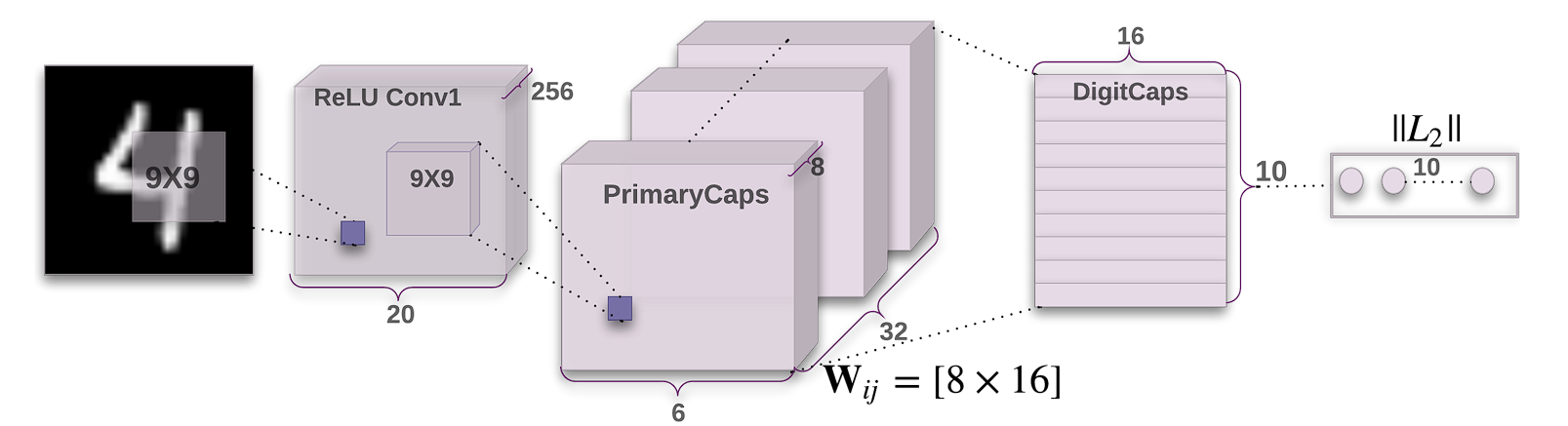
Unlike deep convolutional networks, the original architecture of the Capsule Network proposed has a relatively simple structure comprising 3 layers only.
- Conv1: This is a standard convolutional layer with:
- 256 filters (kernels)
- Kernel size: 9×9
- Stride: 1
- Activation function: ReLU
- Purpose: Extract low-level features from the input image.
- PrimaryCapsules: This is a convolutional capsule layer with:
- 32 channels
- Each capsule contains 8 convolutional units with a 9×9 kernel and a stride of 2. (So each capsule output is an 8-dimensional vector)
- Each capsule “sees” outputs from all Conv1 units whose receptive fields overlap with its location.
- Purpose: Processes the features from Conv1 and groups them into potential entities (like parts of digits).
- DigitCaps: This is the final layer with:
- 10 capsules (one for each digit class)
- Each capsule is 16-dimensional.
- Routing: Each capsule in PrimaryCapsules sends its output to all capsules in DigitCaps. A dynamic routing algorithm determines how much each PrimaryCapsule contributes to each DigitCapsule.
- Purpose: Represents the presence and pose (specific characteristics) of each digit class in the image.
A Math-Intensive Explanation
- Vector Transformation and Prediction Vector (uj|i): Each lower-level capsule (i.e., capsule i at layer l) produces an output vector ui. This output vector is then multiplied by a weight matrix (Wij) to produce a prediction vector (uj|i). This vector is essentially the capsule i’s prediction of the output of capsule j at the next higher layer (l+1). This process is represented by the equation uj|i = Wijui
- Coupling Coefficient (cij) and Agreement: The coupling coefficient (cij) represents the lower degree of agreement between lower-level capsule i and higher-level capsule j. If a lower-level capsule’s prediction agrees with the higher-level capsule’s actual output, their coupling coefficient is increased, strengthening their connection. Conversely, if there is disagreement, the coupling coefficient is reduced. The coefficients are then updated iteratively through the routing mechanism.
- Weighted Sum (sj) and squashing function (vj): The total input to a higher-level capsule (j) is a weighted sum of all prediction vectors ( uj|i) from the capsules in the layer below, weighted by their respective coupling coefficients ( cij). This is represented by the equation sj = Σi=1 to N cijuj|i the vector sj is then passed through the squashing function to produce the output vector vj of capsule j. This squashing function ensures that the length of the output vector i is between o and 1, which allows the network to capture probabilities.
Challenges and Limitations
- Computational Complexity: Dynamic routing, the core mechanism for part-whole understanding in Capsule Networks, is computationally expensive. The iterative routing process and agreement calculations require more resources compared to CNNs. This leads to slower training and increased hardware demand.
- Limited Scalability: CapsNets haven’t been as extensively tested on very large datasets as CNNs. Their computational complexity might become a significant hurdle for scaling to massive datasets in the future.
- Early Stage of Research and Community Support: CapsNets are relatively new compared to CNNs. This also leads to fewer implementations and less community support. This can make implementing Capsule Networks difficult.
Applications of Capsule Networks
- Astronomy and Autonomous Vehicles: CapsNets are being explored for classifying celestial objects and enhancing the perception systems in self-driving cars.
- Machine Translation, Handwritten, and Text Recognition: They show promise in natural language processing tasks and recognizing handwritten texts, which can improve communication and automation in data processing.
- Object Detection and Segmentation: In complex scenes where multiple objects interact or overlap, CapsNets can be particularly useful. Their ability to maintain information about spatial hierarchies enables more effective segmentation of individual objects and detection of their boundaries, even in crowded or cluttered images.
- 3D Object Reconstruction: Capsule Networks have potential applications in 3D object reconstruction from 2D images, due to their ability to infer spatial relationships and object poses, which contribute to more accurate reconstruction of 3D models from limited viewpoints.
- Augmented Reality (AR): Capsule Networks have the potential to revolutionize AR by improving object recognition, spatial reasoning, and interaction in augmented environments, leading to more immersive and realistic AR experiences.