Machine learning is a key domain of Artificial Intelligence that creates algorithms and training models. Two important problems that machine learning tries to deal with are Regression and Classification. Many machine Learning algorithms perform these two tasks. However, algorithms like Linear regression make assumptions about the dataset. These algorithms may not work properly if the dataset fails to satisfy the assumptions. The Decision Tree algorithm is independent of such assumptions and works fine for both regression and classification tasks.
What is a Decision Tree?
Decision Tree is a tree-based algorithm. Both classification and regression tasks use this algorithm. It works by creating trees to make decisions based on the probabilities at each step. This is called recursive partitioning.
This is a non-parametric and supervised learning algorithm. It doesn’t make assumptions about the dataset and requires a labeled dataset for training. It has the structure as shown below:
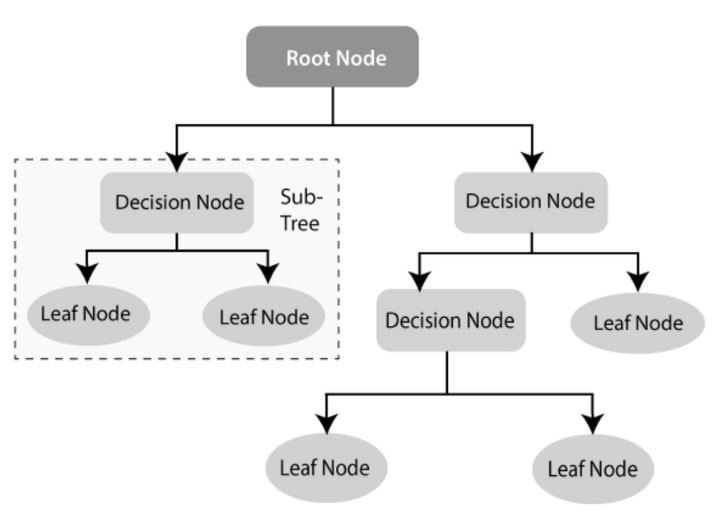
As we can see in the above tree diagram structure, the Decision tree algorithm has several nodes. They are classified as below.
- Root Node: The decision tree algorithm starts with the Root Node. This node represents the complete dataset and gives rise to all other nodes in the algorithm.
- Decision Node/Internal Node: These nodes are based on the input features of the dataset and are further split into other internal nodes. Sometimes, these can also be called parent nodes if they split and give rise to further internal nodes which are called child nodes.
- Leaf Node/Terminal Node: This node is the end prediction or the class label of the decision tree. This node doesn’t split further and stops the tree execution. The Leaf node represents the target variable.
How Does a Decision Tree Work?
Consider a binary classification problem of predicting if a given customer is eligible for the loan or not. Let’s say the dataset has the following attributes:
| Attribute | Description |
|---|---|
| Job | Occupation of the Applicant |
| Age | Age of Applicant |
| Income | Monthly Income of the Applicant |
| Education | Education Qualification of the Applicant |
| Marital Status | Marital Status of the Applicant |
| Existing Loan | Whether the Applicant has an existing EMI or not |
Here, the target variable determines whether the customer is eligible for the loan or not. The algorithm starts with the entire dataset as the Root Node. It splits the data recursively on features that give the highest information gain.
This node of the tree gives rise to child nodes. Trees represent a decision.
This process continues until the criteria for stopping is satisfied, which is decided by the max depth. Building a decision tree is a simple process. The image below illustrates the splitting process on the attribute ‘Age’.
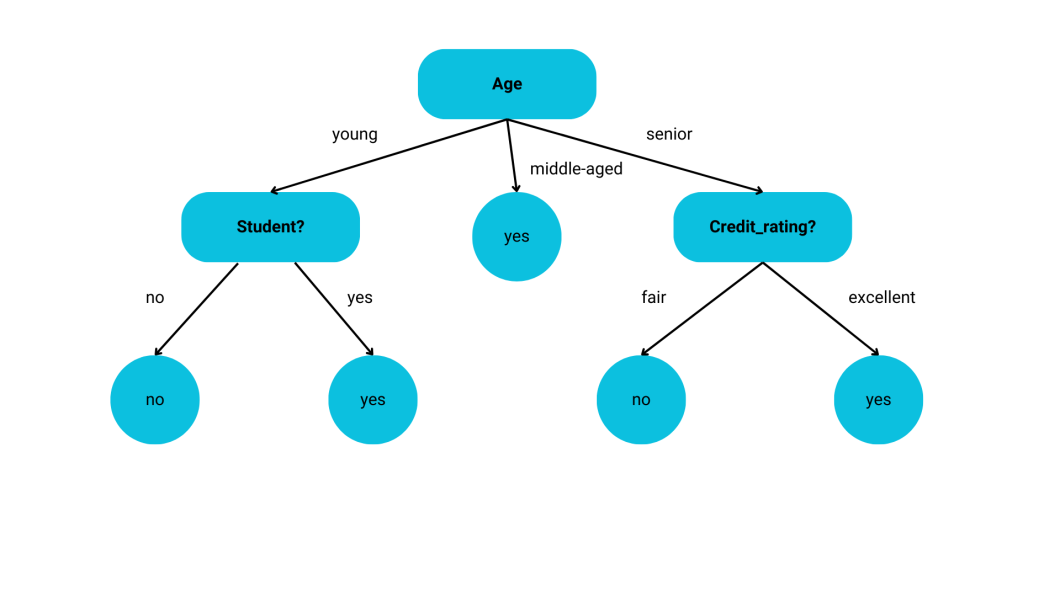
Different values of the ‘Age’ attribute are analyzed, and the tree is split accordingly. However, the criteria for splitting the nodes need to be determined. The algorithm doesn’t understand what each attribute means.
Hence, it needs a value to determine the criteria for splitting the node.
Splitting Criteria for Decision Tree
Decision tree models are based on tree structures. So, we need some criteria to split the nodes and create new nodes so that the model can better identify the useful features.
Information Gain
- Information gain is the measure of the reduction in Entropy at each node.
- Entropy is the measure of randomness or purity at the node.
- The formula of Information Gain is, Gain(S,A) = Entropy(S) -∑n(i=1)(|Si|/|S|)*Entropy(Si)
- {S1,…, Si,…,Sn} = partition of S according to value of attribute A
- n = number of attribute A
- |Si| = number of cases in the partition Si
- |S| = total number of cases in S
- The formula of Entropy is, Entropy=−∑i1=cpilogpi
- A node splits if it has the highest information gain.
Gini Index
- The Gini index is a measure of the impurity in the dataset.
- It utilizes the probability distribution of the target variables for calculations.
- The formula for the Gini Index is Gini(S)=1−∑pi2
- Classification and regression decision tree models use this criterion for splitting the nodes.
Reduction in Variance
- Variance Reduction measures the decrease in variance of the target variable.
- Regression tasks mainly use this criterion.
- When the Variance is minimum, the node splits.
Chi-Squared Automatic Interaction Detection (CHAID)
- This algorithm uses the Chi-Square test.
- It splits the node based on the response between the dependent variable and the independent variables.
- Categorical variables such as gender and color use these criteria for splitting.
A decision tree model builds the trees using the above splitting criteria. However, one important problem that every model in machine learning is susceptible to is over-fitting. Hence, the Decision Tree model is also prone to over-fitting. In general, there are many ways to avoid this. The most commonly used technique is Pruning.
What is Pruning?
Trees that do not help the problem we are attempting to solve occasionally begin to grow. These trees may perform well on the training dataset. However, they may fail to generalize beyond the test dataset. This results in over-fitting.
Pruning is a strategy for preventing the development of unnecessary trees. It prevents the tree from growing to its maximum depth. Pruning, in basic words, allows the model to generalize successfully on the test dataset, decreasing overfitting.
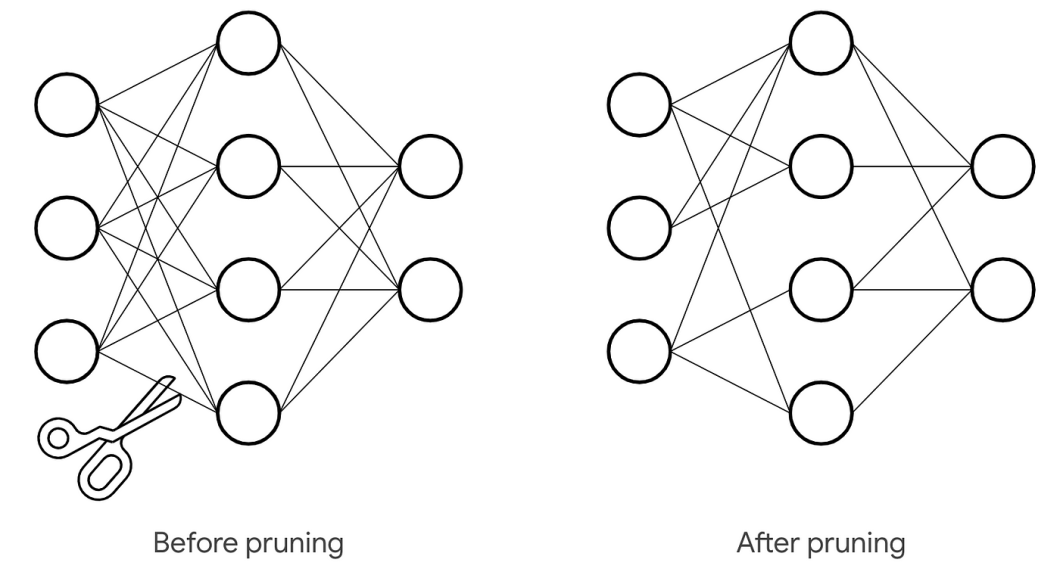
But how do we prune a decision tree? There are two pruning techniques.
Pre-Pruning
This technique involves stopping the growth of the decision tree at early stages. The tree doesn’t reach its full depth. So, the trees that don’t contribute to the model don’t grow. This is also known as ‘Early Stopping’.
The growth of the tree stops when the cross-validation error doesn’t decrease. This process is fast and efficient. We stop the tree at its early stages by using the parameters, ‘min_samples_split‘, ‘min_samples_leaf‘, and ‘max_depth‘. These are the hyperparameters in a decision tree algorithm.
Post-Pruning
Post-pruning allows the tree to grow to its full depth and then cuts down the unnecessary branches to prevent over-fitting. Information gain or Gini Impurity determines the criteria to remove the tree branch. ‘ccp_alpha‘ is the hyperparameter used in this process.
Cost Complexity Pruning (CCP) controls the size of the tree. The number of nodes increases with the increase in ‘ccp_alpha‘.
These are some of the methods to reduce over-fitting in the decision tree model.
Python Decision Tree Classifier
We will use the 20 newsgroups dataset in the scikit-learn’s dataset module. This dataset is a classification dataset.
1. Import all the Necessary Modules
from sklearn.datasets import fetch_20newsgroups from sklearn.feature_extraction.text import CountVectorizer from sklearn.tree import DecisionTreeClassifier from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score
2. Load the Dataset
# Load the 20 Newsgroups dataset newsgroups = fetch_20newsgroups(subset='all') X, y = newsgroups.data, newsgroups.target
3. Vectorize the Text Data
# Convert text data to numerical features vectorizer = CountVectorizer() X_vectorized = vectorizer.fit_transform(X)
4. Split the Data
# Split the dataset into training and testing sets X_train, X_test, y_train, y_test = train_test_split(X_vectorized, y, test_size=0.2, random_state=42)
5. Create a Classifier and Train
# Create and train the decision tree classifier clf = DecisionTreeClassifier(random_state=42) clf.fit(X_train, y_train)
6. Make Accurate Predictions on Test Data
# Make predictions on test data y_pred = clf.predict(X_test)
7. Evaluate the Model Using the Accuracy Score
# Evaluate the model on the test set
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")
The above code would produce a model that has an ‘accuracy_score’ of 0.65. We can improve the model with hyperparameter tuning and more pre-processing steps.
Python Decision Tree Regressor
To build a regression model using decision trees, we will use the diabetes dataset available in Scikit Learn’s dataset module. We will use the ‘mean_squared_error‘ for evaluation.
1. Import all the necessary modules
from sklearn.datasets import load_diabetes from sklearn.tree import DecisionTreeRegressor from sklearn.model_selection import train_test_split from sklearn.metrics import mean_squared_error
2. Load the dataset
# Load the Diabetes dataset diabetes = load_diabetes() X, y = diabetes.data, diabetes.target
This dataset doesn’t have any text data and has only numeric data. So, there is no need to vectorize anything. We will split the data for training the model.
3. Split the dataset
# Split the dataset into training and testing sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
4. Create a Regressor and train
# Create and train the decision tree regressor reg = DecisionTreeRegressor(random_state=42) reg.fit(X_train, y_train)
5. Make accurate predictions on test data
# Make predictions on test data y_pred = reg.predict(X_test)
6. Evaluate the model
# Evaluate the model on the test set
mse = mean_squared_error(y_test, y_pred)
print(f"Mean Squared Error: {mse:.2f}")
The regressor will give a mean squared error of 4976.80. This is pretty high. We can optimize the model further by using hyperparameter tuning and more pre-processing steps.
Real-Life Use Cases With Decision Trees
The Decision Tree algorithm is tree-based and can be used for both classification and regression tree applications. A Decision tree is a flowchart-like decision-making process, making it an easy algorithm to comprehend. As a result, it is used in several domains for classification and regression applications. It is applied in domains such as:
Healthcare
Since decision trees are tree-based algorithms, they determine a disease and its early diagnosis by analyzing the symptoms and test results in the healthcare sector. They can assist in treatment planning and optimizing medical processes. For example, we can compare the side effects and the cost of different treatment plans to make informed decisions about patient care.
Banking Sector
Decision trees can build a classifier for various financial use cases. We can detect fraudulent transactions and the loan eligibility of customers using a decision tree classifier. We can also evaluate the success of new banking products using the tree-based decision structure.
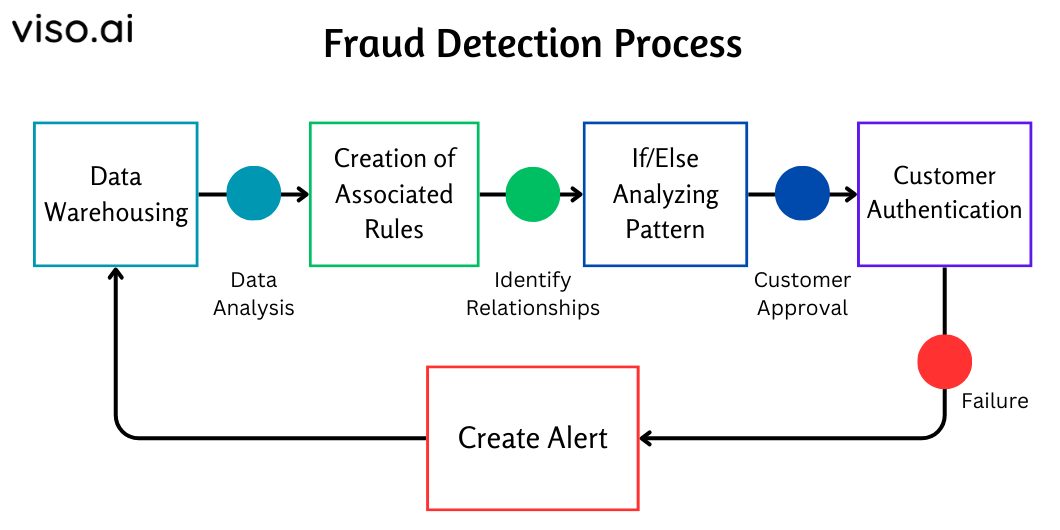
Risk Analysis
Decision Trees are used to detect and organize potential risks, something valuable in the insurance world. This allows analysts to consider various scenarios and their implications. It can be used in project management, and strategic planning to optimize decisions and save costs.
Data Mining
Decision trees are useful for regression and classification tasks. They are also used for feature selection to identify significant variables and eliminate irrelevant features. They can handle missing values and model non-linear relationships between various variables.
Machine Learning as a field has evolved in different ways. If you are planning to learn machine learning, then starting your learning with a decision tree is a good idea as it is simple and easy to interpret. Decision Trees can be applied with other algorithms using ensembling, stacking, and staging which can improve the performance of the model.
